PINNs Part 2: Solving the Hyrdogen Atom Schrödinger Equation
08/24/2024
What interests me most about the physics informed neural network (PINN) is the ability to apply it to all sorts of different physical phenomena that are explained by differential equations. If you haven't read my interpretation and intro to the PINN, check it out here. The original paper claims that the PINN is applicable to general non-linear partial differential equations. I decided to see if I could get a PINN to learn to solve the Schrödinger equation applied to the Hydrogen atom in 3D. This equation is a linear eigenvalue equation, so I have to make a few adjustments to the methods applied in the original paper. I elucidate my reasons for picking this problem below.
The complete Python implementation of everything discussed in this writeup can be found here on GitHub.
Atoms, particles, and the Schrödinger equation
At a fundemental level, everything we humans interact with on a daily basis is some conglomeration of atoms. Atoms make up stuff. All stuff that is stuff, is composed of atoms which interact with each other in interesting and unintuitive ways. An atom consists of neutrons, protons, and electrons, all bound to each other within some space. Every atom has a nucleus that contains neutron(s) and proton(s) that is surrounded by a "cloud" of electron(s). The electron is a fundamental particle of nature and its behavior is the focus of this writeup.
In the world of quantum mechanics, reality is strange and probabilistic. When talking about a particle that follows the laws of quantum mechanics, you can't say where the particle is and what it is doing, but where it probably is and what it probably is doing. All information and derivations in the following section come mostly from Introduction to Quantum Mechanics (Third Edition) by David J. Griffiths and Darrell F. Schroeter, a surpirsingly readable textbook.
A particle is defined by its wavefunction, $\Psi$. The wavefunction is defined by the time-dependent Schrödinger equation
$$\begin{eqnarray}i \hbar \frac{\partial}{\partial t} \Psi = \hat{H}\Psi ,\end{eqnarray}$$
where $i$ is the imaginary number, $\hbar$ is the reduced Planck's constant, and $\hat{H}$ is the Hamiltonian operator. Solving this equation for $\Psi$ gives the state of the particle which can be operated on to determine the probability of its position and momentum. Where this equation comes from is beyond the scope of this writeup, but if you're so inclined, you can read Schrödinger's original proposal of the equation here (though, you may need to have read a quantum mechanics textbook to get what he's talking about, and even then, it's still not simple).
For more reasons I won't explain, a separation of variables allows the Schrödinger equation to be split into different position and time-dependent terms. I'll skip some more details and tell you that the time-independent (and position-dependent) Schrödinger equation is
$$\begin{eqnarray} \hat{H}\psi = E\psi , \end{eqnarray}$$
where $\psi$ is the time-independent wave function and $E$ is the energy eigenvalue. This writeup only focuses on the time-independent Schrödinger, but I plan on coming back to the time-dependent version later.
This PDE can be solved by finding an eigenfunction $\psi$ and its corresponding eigenvalue $E$. Notice that we will look for a solution, not the solution. That is because this is a linear PDE. When a PDE is linear, it basically means that if you find a solution, you can multiply that solution by some constant and get another solution, meaning there are infinitely many solutions (since there are infinitely many constants).
Everything to come will focus on the Schrödinger equation applied to the single electron in the Hydrogen atom, though the theory described applies to all atoms.
The Hamiltonian operator for Hydrogen is defined as
$$\begin{eqnarray} \hat{H} = -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r}) , \end{eqnarray}$$
where $\nabla^2$ is the Laplace operator, $m$ is the mass of the electron, and $V(\vec{r})$ is the potential of the electron defined by
$$\begin{eqnarray} V(\vec{r}) = -\frac{e^2}{4 \pi \varepsilon_0 |\vec{r}|} , \end{eqnarray}$$
where $\vec{r}$ is the position of the electron in 3D cartesian coordinates, $e$ is the charge of the electron, and $\varepsilon_0$ is the permittivity of free space.
When $\hat{H}$ is applied to $\psi$ and all terms in the Schrödinger equation are moved to equate to $0$, we get:
$$\begin{eqnarray} -\frac{\hbar^2}{2m}(\frac{\partial^2 \psi}{\partial x^2} + \frac{\partial^2 \psi}{\partial y^2} + \frac{\partial^2 \psi}{\partial z^2}) - \frac{e^2}{4 \pi \varepsilon_0 |\vec{r}|}\psi - E\psi = 0 . \end{eqnarray}$$
If you read part 1, you probably just said "oh my god he's going to use that as a loss term!" and you would be correct. Except, not exactly, yet. First, let's look at the time-independent Schrödinger equation in spherical coordinates:
$$\begin{eqnarray}\hat{H}\psi(r, \theta, \phi) = E \psi(r, \theta, \phi) . \end{eqnarray}$$
Why use spherical coordinates? Well, the most important reason is because the equation in spherical form has been solved analytically for the Hydrogen atom, while there are no analytical solutions to atoms with more electrons.
Applying $\hat{H}$ to $\psi$ in spherical coordinates gives
$$\begin{eqnarray}-\frac{\hbar^2}{2m} [\frac{1}{r^2} \frac{\partial}{\partial r}(r^2 \frac{\partial \psi}{\partial r}) + \frac{1}{r^2 sin \theta} \frac{\partial}{\partial \theta}(sin \theta \frac{\partial \psi}{\partial \theta}) + \frac{1}{r^2 sin^2 \theta}(\frac{\partial^2 \psi}{\partial \phi^2})] - \frac{e^2}{4 \pi \varepsilon_0 r}\psi = E \psi . \end{eqnarray}$$
Now we can use a separation of variables to split this equation into radial and angular components:
$$\begin{eqnarray}\psi(r, \theta, \phi) = R(r) Y(\theta, \phi) . \end{eqnarray}$$
Skipping some algebra, $R(r)$ and $Y(\theta, \phi)$ are described by
$$\begin{eqnarray} l(l + 1) &=& \frac{1}{R} \frac{d}{dr} (r^2 \frac{dR}{dr}) - \frac{2mr^2}{\hbar^2}[V(r) - E] , \\ -l(l + 1) &=& \frac{1}{Y}[\frac{1}{sin \theta} \frac{\partial}{\partial \theta}(sin \theta \frac{\partial Y}{\partial \theta}) + \frac{1}{sin^2 \theta} \frac{\partial^2 Y}{\partial \phi^2}] , \end{eqnarray}$$
where $l$ is a separation constant defined for reasons I won't detail (this is the angular momentum quantum number, i.e. the $l$ in the $nlm$).
Fortunately, some guys much better than me at math already figured out the solutions to these equations! Arriving at the solutions is a lot of work, however, and I don't feel the need to go through all the math here as countless others have already done so elsewhere. Suffice to say, when solving the above equations, two more constants, $n$ (principal quantum number) and $m$ (magnetic quantum number) are introduced.
The solutions are written
$$\begin{eqnarray} \psi_{nlm}(r, \theta, \phi) = R_{nl}(r) Y^m_l(\theta, \phi) , \end{eqnarray}$$
where
$$\begin{eqnarray} R_{nl}(r) = \sqrt{(\frac{2}{na})^3 \frac{(n - l - 1)!}{2n(n + l)!}}e^{-r/na} (\frac{2r}{na})^l [L^{2l + 1}_{n - l - 1}(2r/na)] , \end{eqnarray}$$
where $a$ is the Bohr radius defined as
$$\begin{eqnarray} a = 0.529 \times 10^{-10} \text{ m}, \end{eqnarray}$$
with the associated Laguerre polynomial and the Laguerre polynomial defined as
$$\begin{eqnarray} L^p_q(x) &\equiv& (-1)^p (\frac{d}{dx})^p L_{p + q}(x) , \\ L_q(x) &\equiv& \frac{e^x}{q!} (\frac{d}{dx})^q (e^{-x}x^q) , \end{eqnarray}$$
and
$$\begin{eqnarray} Y^m_l(\theta, \phi) = \sqrt{\frac{(2l + 1)(l - m)!}{4 \pi (l + m)!}} e^{im \phi} P^m_l(cos \theta) , \end{eqnarray}$$
with the associated Legendre function and the Legendre polynomial defined as
$$\begin{eqnarray} P^m_l(x) &\equiv& (-1)^m (1 - x^2)^{m/2} (\frac{d}{dx})^m P_l(x) , \\ P_l(x) &\equiv& \frac{1}{2^l l!} (\frac{d}{dx})^l (x^2 - 1)^l . \end{eqnarray}$$
Solving the radial equation also gives the energy values
$$\begin{eqnarray} E_n = \frac{-13.6 \text{ eV}}{n^2} . \end{eqnarray}$$
Easy!
In all seriousness, it really wasn't necessary to type out the general analytical solutions here, since you usually just reference a table for a given $nlm$ to get $\psi$, but I wanted to highlight how complicated the analytical solution to the electron wavefunction of the simplest atom is.
As I said earlier, this PDE has infinitely many solutions, but, I first only want to worry about the ground state Hydrogen atom where $n=1$, $l=0$, and $m=0$. Substituting these values into the radial and angular equations gives
$$\begin{eqnarray} R_{10}(r) &=& 2a^{-3/2} e^{-r/a}, \\ Y^0_0(\theta, \phi) &=& (\frac{1}{4 \pi})^{1/2}. \end{eqnarray}$$
This gives the full time-independent ground state wavefunction of the Hydrogen atom
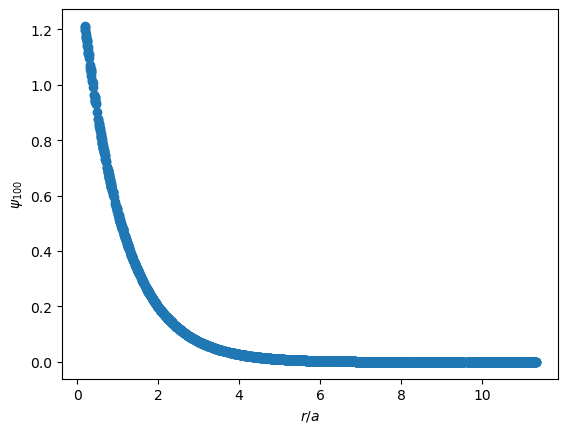
$$\begin{eqnarray} \psi_{100} = 2a^{-3/2} e^{-r/a} (\frac{1}{4 \pi})^{1/2}. \end{eqnarray}$$
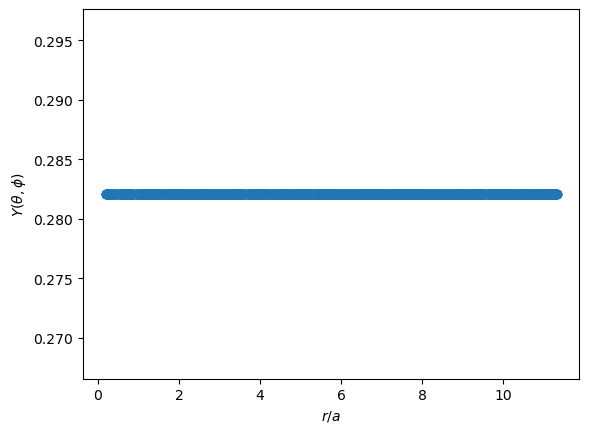
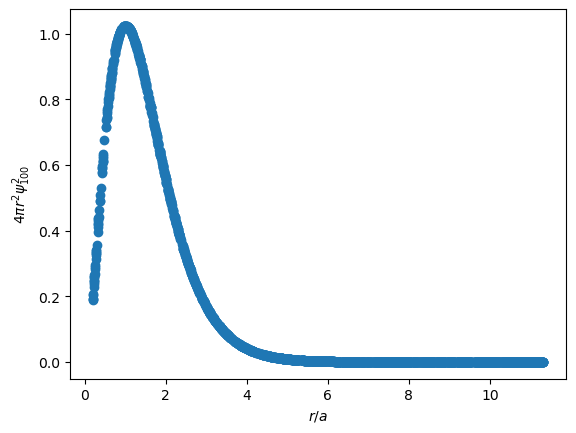
It's important to note that $Y^0_0(\theta, \phi)$ is a constant in the ground state. $\psi_{100}$ is only dependent upon $r$. So, the wavefunction in this state is spherically symmetric, which allows us to define probability densities by multiplying $R(r)^2$ or $\psi(r, \theta, \phi)^2$ by a spherical shell element, $4 \pi r^2 dr$.
The ground state analytical solutions are easy to visualize. First, $2000$ random values of $(r, \theta, \phi)$ are generated in their respective domains $r \in [0.1, 6] \mathring{A}$ (angstroms, equal to $0.1$ nanometers), $\theta \in [0, 2\pi]$, $\phi \in [0, 2\pi]$.
The implementation of the analytical solutions is straightforward:
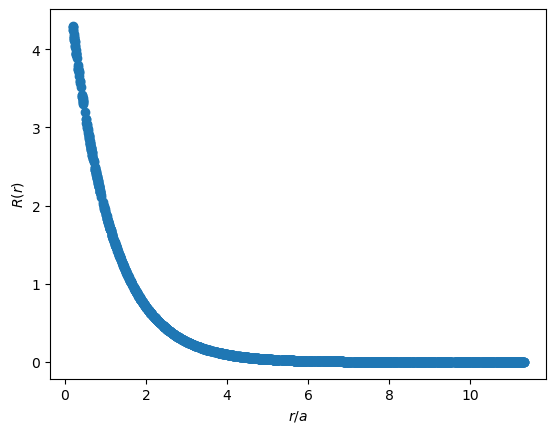
In the plots below, the x axes are presented as $r/a$, a common convention. For the ground state Hydrogen atom, we expect the most likely position of the electron to be located at the Bohr radius, $a$, where $r/a=1$.
The radial function follows exponential decay.
The angular function is constant, of course.
The wavefunction is just a scaled down version of the radial function.
The plot of the probability distribution of the wavefunction effectively says that the electron is most likely between $r/a=0.1$ and $r/a=4$, and unlikely to be found farther away from the nucleus. Integrating this curve between two values of $r/a$ gives the probability of finding the electron between those distances away from the nucleus.
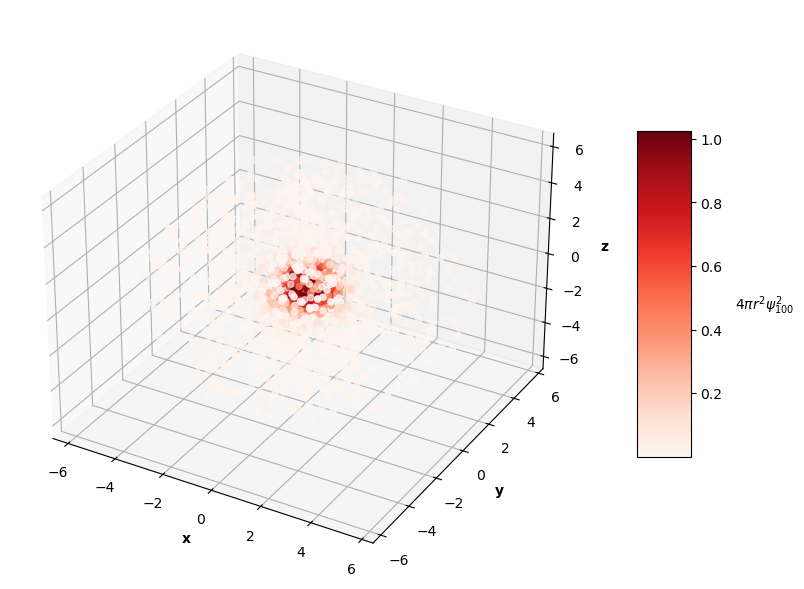
After calculating the values of the wavefunction across various combinations of inputs, the coordinates can be converted back to cartesian, and the probability densities can be visualized in 3D. The color intensity of the plot below shows where the electron is most likely to be found (redder means more likely, lighter means less likely). You can see how the electron's most-likely positions form a dense red sphere around the nucleus at around $r/a=1$ and how its less likely positions become lighter as $r$ increases.
The PINN Approach
What's the point in trying to approximate the H atom Schrödinger equation with a neural network if an analytical solution exists? Well, acquiring the solution is not a straightforward process and is not even possible for atoms that have more than one electron (i.e. every atom that isn't H). I want to solve this equation with a PINN because the approximate solution can be compared to the known analytical solution, and if the PINN approach proves useful for a known problem, I like to think that it could be extended to solve multi-electron atoms that have not been solved analytically.
While reviewing similar work, I came across the paper Physics-Informed Neural Networks for Quantum Eigenvalue Problems by Henry Jin, Marios Mattheakis, and Pavlos Protopapas. This paper discusses approaches for using a PINN to solve various different eigenvalue problems, and provides an approach to solving the radial equation of Hydrogen. This paper introduced me to a few helpful loss terms and a scheme for handling infinite boundary conditions.
Since the Schrödinger is an eigenvalue equation, there are two unknowns to find, the eigenvalue and the eigenfunction. The energy eigenvalue, $E$, can either be a learned input in the PINN or a predicted output. The eigenvalue paper uses the former approach, where $E$ is predicted by an affine layer that takes an input of one(s).
So, a PINN that only predicts the solution to the radial equation given an input $r$ may look something like:
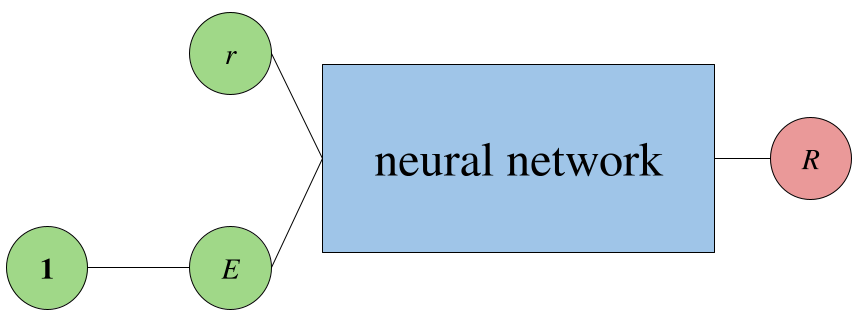
A PINN that predicts $E$ as an output instead would look like:

The goal is to predict the wavefunction of the electron that satisifies the Schrödinger equation given a 3D position. Below, I enumerate a few approaches I have in mind to do so (note that the pattern below is "input $\rightarrow$ neural network $\rightarrow$ output" where the arrows loosely mean "goes to").
1.
$r$, $\theta$, $\phi$ $\rightarrow$ NN $\rightarrow$ $\psi$
2.
$r$ $\rightarrow$ radial NN $\rightarrow$ $R$
$\theta$, $\phi$ $\rightarrow$ angular NN $\rightarrow$ $Y$
from the analytical solution, $\psi = RY$
3.
$r$, $\theta$, $\phi$ $\rightarrow$ NN $\rightarrow$ $R$, $Y$
again, $\psi = RY$
4.
$x$, $y$, $z$ $\rightarrow$ NN $\rightarrow$ $\psi$
Note that in each approach listed above, $E$ could be predicted implicitly and given as an input to the NN, or $E$ could be an output prediction, meaning that there are twice as many approaches as listed above to try. Also note that there are more possible approaches that I haven't mentioned or thought of, but I'm going to start with these and see what I learn, and then hopefully I can refine my options based on what seems to work best.
Also, I'm still only considering the time-independent Schrödinger equation. The time-dependent equation takes a different form and requires its own unique considerations. I figure starting out with the time-independent form will generate the easiest results to interpret and compare to analytical solutions. The time-independent equation can be written in terms of spherical or cartesian coordinates, and I'm not sure which PINN system will produce better results. The advantage of using the spherical form is that $R$ and $Y$ can be compared to their analytical solutions, and then $\psi$ can be evaluated. I feel like this makes the problem a bit simpler for a neural network to solve. However, the cartesian form of the Schrödinger equation looks simpler, subjectively speaking.
Thinking through this problem really makes me wonder how cherry-picked the results in PINNs-related publications are. Maybe cherry-picked isn't the right term, but I can't help but notice how many avenues there are to explore around the "good" approaches that these publications share. When I replicated the approaches from the original PINNs paper and the quantum PINNs paper, it was very easy to miss or change one little thing in the PINN system and observe the neural net's predictions turn unstable or become completely wrong. I guess what I'm trying to say is that it would be nice if authors shared more of the failed experiments that led to their "good" results.
Well, this isn't a publication, so I'm just going to share everything I can, good and bad.
Neural network architectures
Up to this point, I've only referred to a generic neural network and haven't detailed any specific architectures. The original PINNs paper used linear layers with tangent activation functions and the quantum PINNs paper used linear layers with sin activation functions. I'm going to assume that if I put enough linear layers together with any activation function, I'll see results (see my writeup on the universal function approximation theorem). When it comes to architecture selection, it is common to make a choice based on the type of data being modeled (i.e. CNNs are good for images, transformers are good for text, etc...) and tweak from there. From what I've read, I don't see a consensus on specific architectures consistently outperforming others on physics PDE problems, so I'll start with a simple architecture of linear layers and make alterations to it as I experiment.
Loss functions
Once the net has made a prediction, the physics of the problem is used to determine how wrong the prediction is. Regardless of which PINN approach is used, there are several expectations for the output prediction(s).
First and foremost, the output prediction should satisfy the Schrödinger equation ($DE$ means differential equation below, I use the same notation as the quantum PINNs paper). When all terms of the Schrödinger are moved to one side, they should equate to $0$. On $N$ predictions, the mean of the output predictions substituted into the Schrödinger equation squared is taken to quantify how well the PINN has learned to satisfy the constraints of the differential equation.
For the cartesian approach, one loss term is defined (note that $i$ refers to the $i$th prediction and $\hat{E_i}$ is constant across all predictions if it is learned implicitly in the net):
$$\begin{eqnarray} L_{DE, \psi} = \frac{1}{N} \sum_{i=0}^N [-\frac{\hbar^2}{2m}(\frac{\partial^2 \hat{\psi_i}}{\partial x^2} + \frac{\partial^2 \hat{\psi_i}}{\partial y^2} + \frac{\partial^2 \hat{\psi_i}}{\partial z^2}) - \frac{e^2}{4 \pi \varepsilon_0 |\vec{r_i}|}\hat{\psi_i} - \hat{E_i}\hat{\psi_i}]^2 . \end{eqnarray}$$
For the spherical approach, there are three loss terms worth considering. The usage of each will be discussed later. First, there is the full Schrödinger equation:
$$\begin{eqnarray} L_{DE, \psi} = \frac{1}{N} \sum_{i=0}^N \{-\frac{\hbar^2}{2m} [\frac{1}{r_i^2} \frac{\partial}{\partial r}(r_i^2 \frac{\partial \hat{\psi_i}}{\partial r}) + \frac{1}{r_i^2 sin \theta_i} \frac{\partial}{\partial \theta}(sin \theta_i \frac{\partial \hat{\psi_i}}{\partial \theta}) + \frac{1}{r_i^2 sin^2 \theta_i}(\frac{\partial^2 \hat{\psi_i}}{\partial \phi^2})] - \frac{e^2}{4 \pi \varepsilon_0 r_i}\hat{\psi_i} - E \hat{\psi_i}\}^2 , \end{eqnarray}$$
there's also the radial equation:
$$\begin{eqnarray} L_{DE, R} = \frac{1}{N} \sum_{i=0}^N \{ l(l + 1) - \frac{1}{\hat{R}} \frac{d}{dr} (r_i^2 \frac{d\hat{R}}{dr}) - \frac{2mr_i^2}{\hbar^2}[V(r_i) - E] \}^2 ,\end{eqnarray}$$
and the angular equation:
$$\begin{eqnarray} L_{DE, Y} = \frac{1}{N} \sum_{i=0}^N \{ -l(l + 1) - \frac{1}{\hat{Y}}[\frac{1}{sin \theta_i} \frac{\partial}{\partial \theta}(sin \theta_i \frac{\partial \hat{Y}}{\partial \theta}) + \frac{1}{sin^2 \theta_i} \frac{\partial^2 \hat{Y}}{\partial \phi^2}] \}^2 .\end{eqnarray}$$
It's important to remember that the neural network will try to learn a solution, not the solution because there are infinitely many solutions to linear eigenvalue equations. The quantum PINNs paper presents some methods to handle finding multiple solutions, but I'll come back to that later when it's more relevant.
Without giving the details explaining why, wavefunctions that solve the Schrödinger equation must be orthonormal to one another. This means that if you take the inner product of a wavefunction with itself, you should get $1$, and if you take the inner product between a wavefunction and any other wavefunction that solves the same Schrödinger equation, you should get $0$. So, if values that span the domains of the wavefunction's possible inputs are passed into the PINN and a vector of predictions $\hat{\psi}$ is produced, the dot product of that vector with itself should equal $1$. So, the network should minimize the term:
$$\begin{eqnarray} L_{norm} = \hat{\psi} \cdot \hat{\psi} .\end{eqnarray}$$
The neural net's goal is to minimize these loss terms, but, the easiest way to get these loss terms to $0$ is to simply predict $\hat{\psi}=0$, the trivial solution. This answer isn't helpful because we know the wavefunction is non-zero as the electron must be somwhere. Similarly, $\hat{E}$ shouldn't be $0$ either. To penalize $0$ predicitons, I will use:
$$\begin{eqnarray} L_{non \text{-} triv} = \frac{1}{\hat{\psi}} + \frac{1}{\hat{E}} .\end{eqnarray}$$
The overall loss of the PINN is defined as the sum of the aforementioned loss terms. Depending on the approach, the terms included in the sum differ.
Data generation
From the analytical solution of the radial equation, it's known that the electron is almost definitely within $\text{10 } \mathring{A}$ ($1$ nanometer) of the nucleus in the ground state H atom. The electron is most likely to be found $\text{0.529 } \mathring{A}$ (the Bohr radius, $a$) away from the nucleus in this state. So, I've somewhat arbitrarily decided that the data to train the network on will consist of points in 3D space within $\text{6 } \mathring{A}$ of the nucleus since positions beyond this distance are not worth practical consideration.
I generate data points for training/testing using the same random sampling method used for the $(r, \theta, \phi)$ data described earlier in the analytical solution section. For the networks that require cartesian coordinates, I simply use the same spherical data generation method and then convert the values to cartesian with the following function.
The data generated has units of $\mathring{A}$, the output $\hat{\psi}$ is unitless, and I decided that $\hat{E}$ will have units of $\text{eV}$. I'm not totally sure if this is necessary (or if there's a more clever approach), but I've decided to put the constant terms $\frac{\hbar^2}{2m}$ and $\frac{e^2}{4 \pi \varepsilon_0}$ from the Schrödinger equation in units of $\text{eV}$, $\text{s}$, $\text{kg}$, and $\mathring{A}$. From what I can tell, I could just call each of these constant terms $1$ without loss of generality (i.e. if the PINN method is successful, it can still be used for the appropriate constants), but I'd just like to keep valid units. Conversion time! (Note that I somewhat arbitrarily round/drop significant figures on values below, and it's not a big deal.)
The reduced Planck constant, $\hbar$, is commonly given in the desired units:
$$\begin{eqnarray} \hbar = 6.5821 \times 10^{-16} \text{ eV} \cdot \text{s}.\end{eqnarray}$$
The mass of the electron is also commonly given in $\text{kg}$:
$$\begin{eqnarray} m = 9.1093 \times 10^{-31} \text{ kg}.\end{eqnarray}$$
So, we get the value
$$\begin{eqnarray} \frac{\hbar^2}{2m} = 0.2378 \text{ eV}^2 \cdot \text{s}^2 \cdot \text{kg}^{-1}.\end{eqnarray}$$
The next term, $\frac{e^2}{4 \pi \varepsilon_0}$, requires a bit more manipulation to get the desired units. The charge of the electron is given as
$$\begin{eqnarray} e = 1.6022 \times 10^{-19} \text{ C},\end{eqnarray}$$
and the vacuum permittivity constant, $\varepsilon_0$, is given as
$$\begin{eqnarray} \varepsilon_0 = 8.8542 \times 10^{-12} \text{ C}^2 \cdot \text{kg}^{-1} \cdot \text{m}^{-3} \cdot \text{s}^2.\end{eqnarray}$$
Meters are converted to Angstroms by multiplying $\varepsilon_0$ by a factor $1 \times 10^{-30}$, by the fact that:
$$\begin{eqnarray} \frac{\text{C}^2 \cdot \text{s}^2}{\text{kg} \cdot \text{m}^3} \cdot \frac{(1 \text{ m})^3}{(1 \times 10^{10} \mathring{A})^3} = \frac{\text{C}^2 \cdot \text{s}^2}{\text{kg} \cdot \mathring{A}^3} \cdot \frac{1}{1 \times 10^{30}} .\end{eqnarray}$$
So,
$$\begin{eqnarray} \varepsilon_0 = 8.8542 \times 10^{-42} \text{ C}^2 \cdot \text{kg}^{-1} \cdot \mathring{A}^{-3} \cdot \text{s}^2.\end{eqnarray}$$
Now we can write
$$\begin{eqnarray} \frac{e^2}{4 \pi \varepsilon_0} = 230.7142 \text{ kg} \cdot \mathring{A}^3 \cdot \text{ s}^{-2}.\end{eqnarray}$$
Using Angstroms and electronvolts gives the Schrödinger equation constants reasonable orders of magnitude, which allows for simpler handling in code and easier prediction interpretation.
It is best practice to split datasets into batches when training a neural network. After each batch passes through the net, losses are calculated and the net's parameters are updated. This typically allows the network to learn to make better predicitons. With the data generated, batching is a simple reshape:
Now, the data is generated and batched using the functions already defined:
The best approach
As I've already discussed, there are many different PINN approaches to this problem, and for each approach there are an endless amount of experiments to try (network architectures, network hyperparamters, different combinations of loss functions, etc...). Since the space of potentially valid approaches here is huge, I decided to only implement what I felt were the best options for success.
After a large number of failures and 50+ hours of training (each model version I tried took around 15-60 minutes to train on my PC), I can confidently say that I have yet to achieve great results.
That being said, some results certainly look a lot better than others, and a subset of those results suggest that the model learned to predict something close to the expected outcome.
The best result uses the approach:
$r$, $E$ (implicit) $\rightarrow$ radial NN $\rightarrow$ $R$
$\theta$, $\phi$ $\rightarrow$ angular NN $\rightarrow$ $Y$
$\psi = RY$
with the loss defined by:
$$\begin{eqnarray} L = L_{DE, \psi} + L_{norm} .\end{eqnarray}$$
The radial neural network consists of a single neuron that predicts $\hat{E}$, which feeds into 3 dense layers of 50 neurons and tanh activation functions, which feed into a final dense layer of 50 neurons that outputs a single value, $\hat{R}$. This network only takes $r$ as an input.
The angular neural networks uses the exact same architecture as the radial neural network, except without the section that generates $\hat{E}$. It takes $\theta$ and $\phi$ as inputs and outputs $\hat{Y}$.
In code, the radial neural network looks like:
Similary, the angular neural network is defined:
These networks are instantiated and called upon inside a main PINN class. This class also handles loss calculation and backpropagation.
Finally, the main training loop is defined:
After 10,000 epochs of training, the following loss plots were obtained:
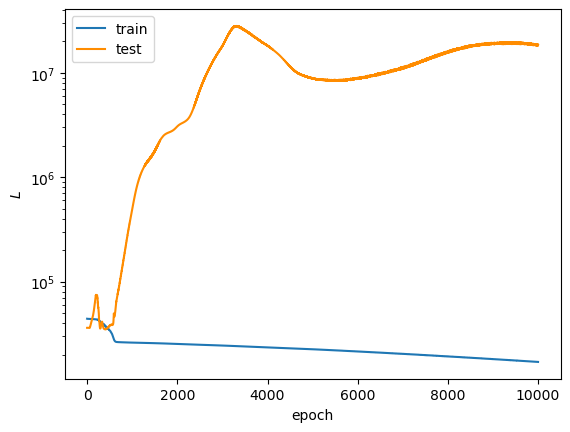
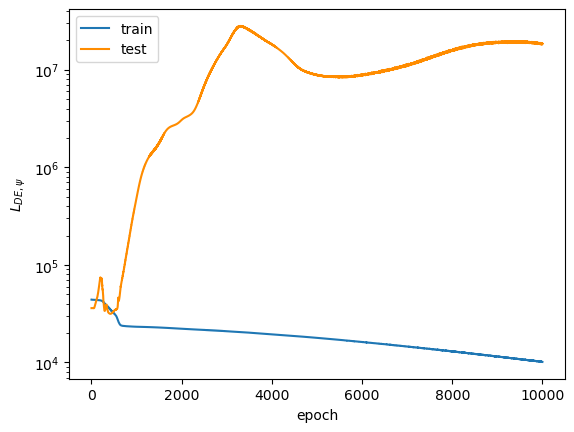
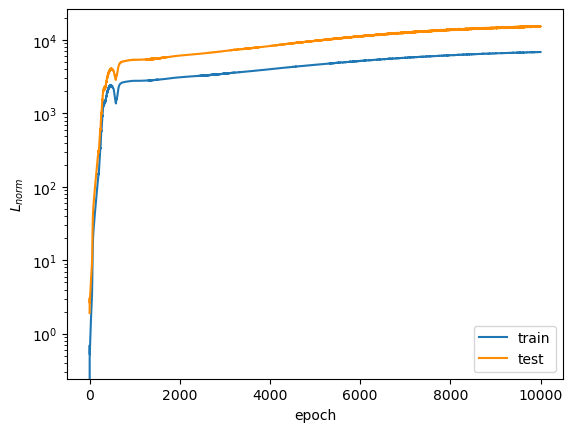
The overall loss does not converge to a small enough value to convince me that the model is a good fit. I honestly don't know why the test $L_{DE, \psi}$ diverged so far from the train $L_{DE, \psi}$. $L_{norm}$ diverges away from $0$ as the epoch number increases, which suggests to me that the model initially learned the trivial solution and then veered away from it, though, I'm not sure why it diverged so far away (final value settled on the order of $10^3$). However, this may not be a correct assumption because the trivial solution prediction would have made $L_{DE, \psi}$ close to $0$ in the early training epochs, while it actually starts on the order of $10^4$. Remember that both of these loss terms are supposed to converge to $0$ across training... So, the model does not look great so far.
Subjectively speaking, the loss plots looked weird and odd in just about every model iteration I trained. By this, I mean I did not consistently see loss curves that decreased across training, as expected for a model that learns well.
Let's take a look at the model's predictions on 2,000 unseen data points.
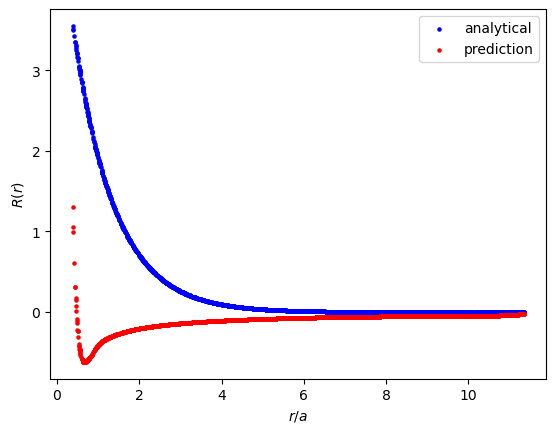
Clearly, the $R$ predictions do not perfectly fit the analytical solution. That being said, the model does predict an initially larger value of $R$ that steeply decays to $0$, which looks like promising behavior. Unfortunately, the model doesn't learn to predict small enough values of $R$ beyond $r/a=6$. The analytical solution produces values of $R$ on the order of $10^{-5}$ at a minimum, whereas the model only predicts values of order $10^{-3}$ at a minimum.
After training many different versions of this PINN, I have consistently seen an inflection point between $r/a=0.3$ and $r/a=1$. Sometimes this inflection point is a maximum and sometimes it's a minimum. Perhaps this is just my imagination, but I feel as though the model learns that there is some significance around this point, and I'm hoping that it's finding the importance of $\psi$ at $r/a=1$ in some non-obvious way. This hope feels similar to looking at a cloud and saying "oh, I see a cat!"
Let's consider the model's predictions for $Y$.
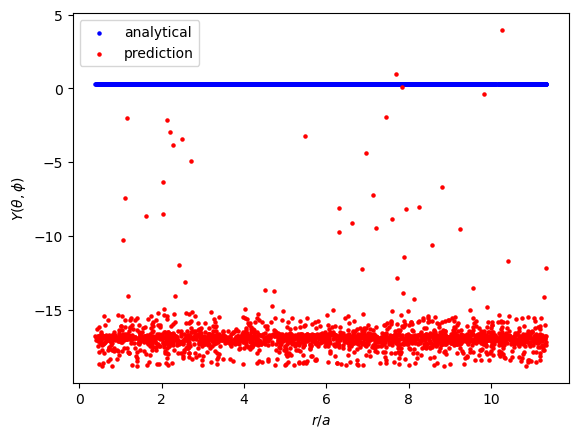
In the analytical solution, $Y$ is a constant that doesn't depend on any input. I expected the model to learn this value easily since the solution is so simple. It appears that the model did roughly learn to predict a constant value across all $r$, but that constant is around -16, when it should be about 0.28.
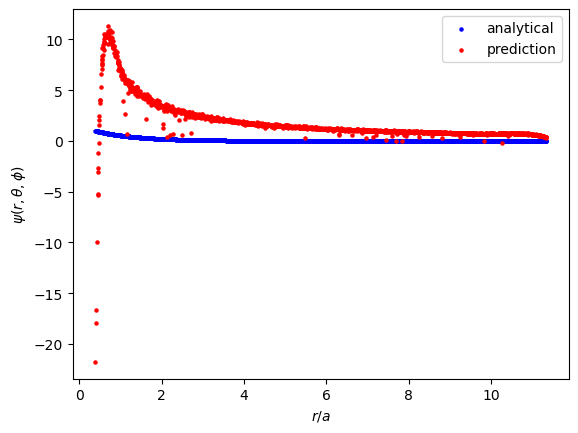
$\psi$ is of course just $RY$. The incorrect order of magnitude in $\hat{Y}$ makes $\hat{\psi}$ much larger than it should be.
The implicit energy prediction across the training epochs:
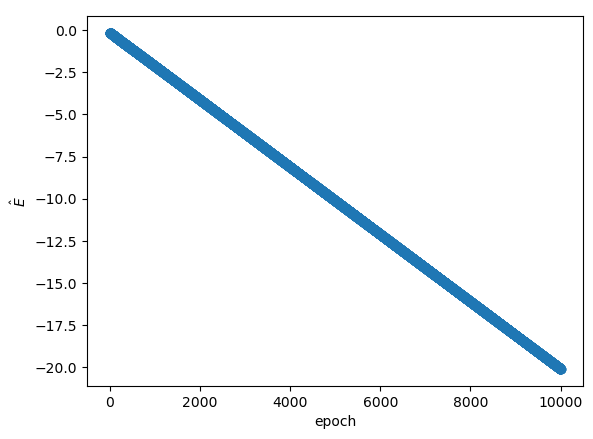
Ideally, this plot would show convergence to $E=-13.6 \text{ eV}$ after enough epochs, but this did not happen in any models trained. I'm not sure why, but every model developed that implicitly predicted $E$ a linear plot of $E$ across the training epochs. The change was always strictly increasing or decreasing across training. This behavior feels wrong to me, but I can't seem to get any different results with this PINN scheme.
The incorrectness in $\hat{Y}$ leads to incorrectness in $\hat{\psi}$, which in turn leads to larger loss values. If $\hat{R}$ were approaching a correct value, an incorrect $\hat{Y}$ would sabotage the model's ability to recognize what a good $\hat{R}$ looks like. This relationship exists in the opposite direction too, of course. The way I've approached this PINN makes the predicitons of $\hat{R}$ and $\hat{Y}$ compete. Throw in an incorrect $\hat{E}$ and the model should have even more difficulty in making good predictions. I tried to avoid these issues by training a network to predict $\hat{R}$ with the analytical values of $Y$ and $E$ given. The network was trained to minimize $L_{DE, R}$ and $L_{norm, R}$ (I did not discuss this loss term earlier, but it is similar to the $L_{norm}$ term already discussed). To my surprise, this approach didn't produce decent results either. I figured with fewer constraints the network would learn $\hat{R}$ easily, but instead it predicted the trivial solution (adding $L_{non \text{-} triv}$ and other loss hacks did not fix the model either). Oddly enough, the amount of constraints and competing interests in the approach discussed in this section produced the best results, even though the results aren't what I had hoped for.
What now?
Welp, I certaintly can't say this project is complete. I've produced results that suggest that my PINN approach for solving the ground state H atom Schrödinger equation isn't completely wrong, but it's not great either.
Beyond the best approach outlined above, I tried every other approach detailed in The PINN Approach. These other trained models predicted the trivial solution or produced seemingly random outputs. Most importantly, the distributions of loss across all models either did not converge or did not converge to a small enough value to convince me of a good model fit.
This is completely subjective, but I just feel like solving this PDE with a neural network is very doable. The solution to the radial equation is just exponential decay, and the solution to the angular equation is just a constant. Intuitively, that's a simple solution. It's just a matter of applying the proper constraints to the network. While reading about other physics-informed machine learning problems, I've realized how far behind I am on the current literature. As I continue to read and learn about other problems in this subfield of computational physics, I expect to uncover insights applicable to solving the problem discussed in this writeup.
I must admit that I wrote all of this mainly for myself as an attempt to summarize the work I've already done and to find mistakes in my thinking. I have found several issues and inconsistencies that I won't detail here, but am using to reconsider parts of my approach. If you read everything here (I'd be surprised) and have any insights/critiques, please contact me.
Despite the lack of decent results, I have had way more fun working on this machine learning project than any other in recent memory and I'm not going to stop working on it until I attain good results or until I thoroughly convince myself that good results are unattainable. I am enamored by the idea of doing something interesting and novel. Let me conclude this writeup by saying that this is part 2 of N, and I don't know what N is yet.